热门政策

这听起来像是您可能在拳击比赛的规则书中找到的内容，但实际上它是指模型执行期间在决策表中选择规则的方式。回想一下，决策表通常包含许多规则，并且在该表的左上角有一个框，其中包含一个字母，指示“ 命中策略” （如何选择规则）。缺省值是决策表中的规则不重叠，但是如果规则确实重叠，这意味着一个以上的规则可以匹配一组给定的输入值，则需要命中策略指示符才能识别表类型并允许决策逻辑要明确理解。根据匹配的规则数量，“命中策略”可以分为两组：

• 选择一个规则（唯一，任意，优先，优先）
• 选择了多个规则（输出顺序，规则顺序，收集）

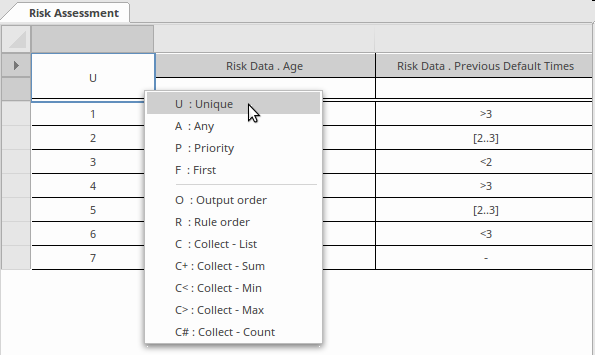
不必太担心每种方法的含义，因为我们将在短期内讨论它们，并提出一些基本的方法来选择一种命中策略而不是另一种命中策略-如果有疑问，请选择唯一（U）策略，因为它是默认策略，也是最常见的策略常用的。 Enterprise Architect支持所有命中策略和验证工具（我们将在下一节中了解）使用命中策略来确定决策表中的规则是否存在间隙或重叠。

选择正确的命中策略对于成功指定决策模型的逻辑级别至关重要。像建模中的许多其他事情一样，实际上，命中策略被更频繁地使用，因为它们被证明是表达特定决策的最佳方法，而其他策略则很少使用，而其他策略则很少使用。命中策略包括字母代码，名称和描述，如下所示。

单一规则匹配政策：

• ûNIQUE（U）：没有重叠是可能的，所有的规则是不相交;只能匹配一个规则（这是默认设置）

• 甲 NY（A）：有可能是重叠的，但所有的匹配规则显示每个输出等于输出条目，所以任何匹配，可以使用

• P riority（P）：多个规则可以匹配，具有不同的输出条目;此策略返回具有最高输出优先级的匹配规则

• 第一 （F）：多个（重叠）规则可以匹配，但具有不同的输出条目；返回按规则顺序的第一个匹配

• 频输出的顺序（O）：返回所有匹配输出递减的优先级顺序

• [R ULE顺序（R）：返回规则顺序全部命中

• Çollect（C）：返回以任意顺序全部命中;可以添加一个运算符（“ +”，“ <”，“>”，“＃”）以将简单函数应用于输出

• + （总和）：决策表的结果是所有不同输出的总和

• < （min）：决策表的结果是所有输出中的最小值

• > （最大值）：决策表的结果是所有输出中的最大值

• ＃ （计数）：决策表的结果是不同输出的数量

独特

具有唯一 （U）命中策略的表定义了一组不重叠的规则，这意味着规则是互斥的，或者在形式集术语中不相交。这意味着对于给定的一组输入，只有一个规则将匹配，并且将产生一组适用的输出。因此，它是单击单输出策略。毫无疑问，它是所有命中策略中最常见的一种，因为它在许多逻辑上下文中都有广泛的应用，每个规则都可以独立推理，并且业务和非技术利益相关者都易于理解。

规则顺序是自由变化的，这意味着规则的顺序不会影响决策的结果。这具有额外的好处，即可以以最大化对决策逻辑的整体理解的方式对规则进行排序，还可以将规则作为独立实体进行开发和推理。

任何

具有“ 任何” （A）命中策略的表定义了一组可能重叠的规则，其中规定，如果它们确实重叠，则输出值相同。因此，这是一个单一命中单一输出策略，这样，一旦规则与所有输入值匹配，就会返回结果，因为任何后续匹配（可能会发生）都将导致相同的输出值。像“ 唯一”这样的“ 任意”策略是非常普遍使用的，它的主要优点和使用它代替“唯一”的原因是，它减少了引入条件以排除规则条件的需求，否则这些条件会导致相同的结果。因此，总是可以使用唯一命中策略创建一个等效表，但是带有ANy策略的表通常是首选，因为它更易于理解，并且创建起来也很繁琐，因为不需要确保每个输入值的排列仅匹配一个规则。

在此示例中，已定义规则的顺序以促进表的可读性，从而使逻辑更加透明。请注意，前三个规则具有相同的结果，并且已进行了排序，以使表的逻辑更加透明。

如果发现原本将使用“唯一”策略的表具有许多重复规则且结果相同，则请考虑使用“任何匹配”策略。这种命中策略的好处之一是，它使决策表更易于理解，并使逻辑更加透明。

优先

具有优先级 （P）命中策略的表定义了一组重叠的规则，这意味着规则可能具有不同的输出。因此，这是单个匹配/单个输出策略，因此，只要规则与所有输入值匹配，就会返回结果，因为任何后续匹配（可能会发生）都将导致相同的输出值。诸如Any之类的优先级策略是非常常用的方法，它的主要优点和使用它代替Any的原因是在存在枚举的输出值列表的情况下。结果在输出列中列出的顺序决定了规则顺序，而选择的规则是优先级最高的规则。

第一

具有优先 （F）命中策略的表定义了一组可能重叠的规则，条件是规则的顺序指定应命中哪个规则。这意味着对于给定的一组输入，将激发表顺序中输入匹配的第一条规则，并将产生结果。因此，它是单击单输出策略。它不常用，并且许多支持者和经验丰富的决策建模者都不愿意使用它，因为它违反了最佳实践规则，即决策表中规则的顺序不应影响结果。但是，对于具有少量规则的表以及在存在一些非常重要且可能不那么频繁出现的条件，这些条件在逻辑上将覆盖任何更频繁出现的次要重要性的输入条件的情况下，它非常有用。