| 前页 | 后页 |
从方程式创建一个约束块
此特征可从Enterprise Architect Release 14. 1中获得。
在开发工程解决方案时,通常要求反映使用数学方程式计算确定的因素,例如力 = 质量 x 加速度(或 f=m*a)。方程由 a约束表示,方程的元素 - 在本例中为f 、 m和a - 是约束的参数。
您可以使用“编辑约束”对话框将一个或多个计算约束模型为块约束块元素,通过该对话框解析约束并从每个约束中提取参数。您可以应用任何适用于您的模型的方程式,无论它们是国际标准公式还是您在工作领域内自己推导出的公式。
访问
|
上下文菜单 |
右击一个约束块|编辑约束块 |
|
其它 |
工具箱、图表块定义页面 |将约束块图标拖放到块定义图上 |
解析方程并创建参数
假设我们有一个名为“Damper”的约束块,包含以下三个方程作为约束:
- v_rel = der(s_rel)
- f = d * v_rel(“d”是“阻尼系数”的错误符号;这是故意的,以便在以后的步骤中进行更正)
- lossPower = f * v_rel
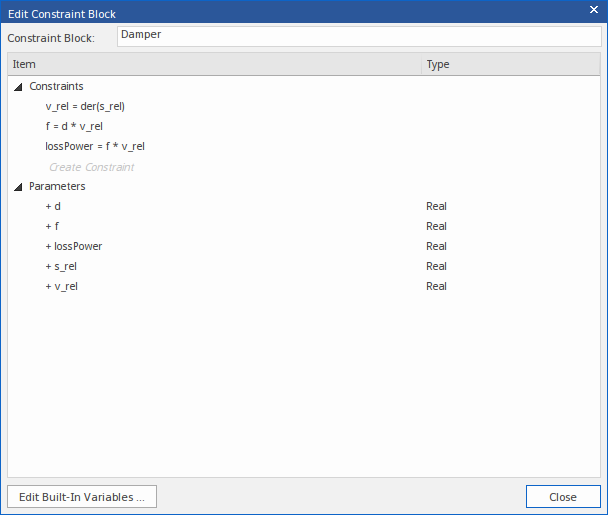
每个参数前面的“+”号表示它在模型中尚不存在。在模型中创建参数:
- 单击关闭按钮。
系统会显示提示以选择是否创建参数。
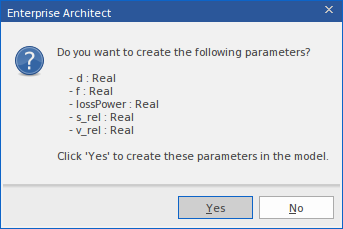
- 单击是按钮。
此图像显示了由此产生的约束块阻尼器。

删除参数
“编辑约束块”对话框也可用于从块中删除约束及其相关参数。
在我们的示例中,假设我们打开对话框并删除约束:
lossPower = f * v_rel
(右键单击约束并选择“删除”选项。)
约束唯一的参数(在本例中为“lossPower”参数)将移动到标题“Not需要”下。
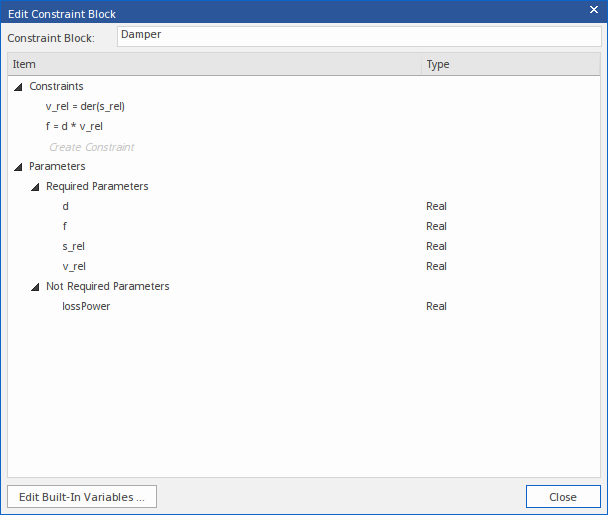
您现在可以:
- 右键单击参数并选择“删除参数”上下文菜单选项,或
- 右键单击“需要参数”标题并选择“删除所有不需要的参数”选项
重命名现有参数
在我们的示例中,假设我们打开对话框并更改约束:
f = d * v_rel
至
f = 阻尼系数 * v_rel
(单击约束,单击约束中的点开始编辑,改写或删除文本。然后单击关闭约束。)
这些变化将发生:
- 提取参数“dampingCoefficient”并报告为新参数(当前模型中不存在)
- 参数“d”报告为“需要”
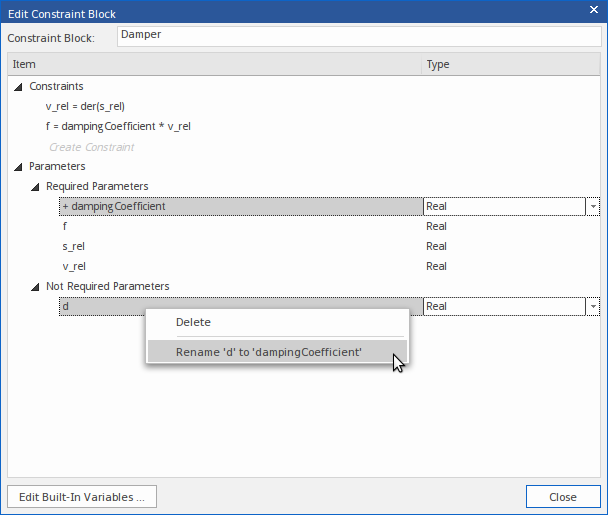
(有关绑定参数的信息,请参阅 ConstraintProperty 的绑定参数帮助主题。)
数学函数
方程解析器支持在约束方程中使用数学函数(如本主题前面的der(s_rel) )。指定函数时,函数名和左括号之间不应有空格。函数参数将被提取为新的约束参数,但函数名称不会。
内置变量
方程可能包含您不希望提取为约束参数的变量。例如,仿真环境 OpenModelica 提供了许多内置变量,因此在 OpenModelica 下要对模型进行仿真时,您不希望将这些变量复制为提取参数。您可以识别“编辑约束块”功能的内置变量,以便它们不会从约束方程中提取,从而避免潜在的冲突。
要定义不应作为参数提取的变量列表,请在“编辑约束块”对话框中单击“编辑内置变量...”按钮。
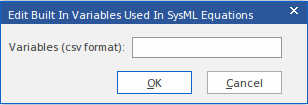
然后输入或添加到以逗号分隔的内置变量名称列表。
例如,OpenModelica 将“时间”定义为内置变量,因此我们将“时间”添加到约束块的列表中。然后当我们输入方程'r = cos (时间)'时,只会提取参数'r'。
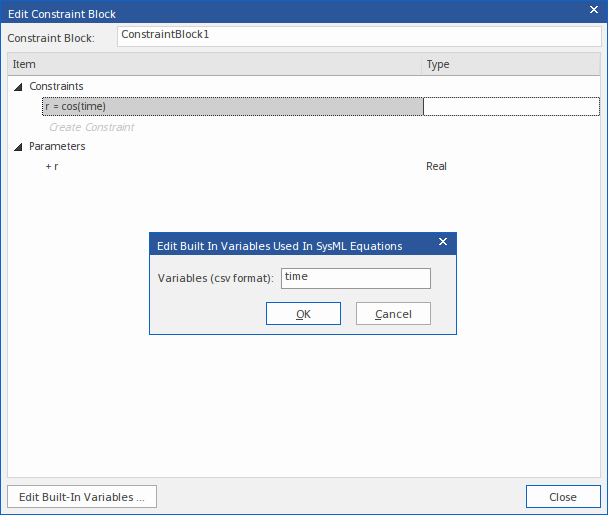
复合约束块
在开发更复杂和/或顺序计算的约束时,您可以构造复合约束块来分解和序列计算。
在这个例子中,ConstraintBlock K本身并没有定义任何约束,而是作为一个组合从它的三个组件 ConstraintBlocks K1 、 K2和K1TimesK2继承它们。 ConstraintBlock K继承了 a、b、c、d 和K五个参数。
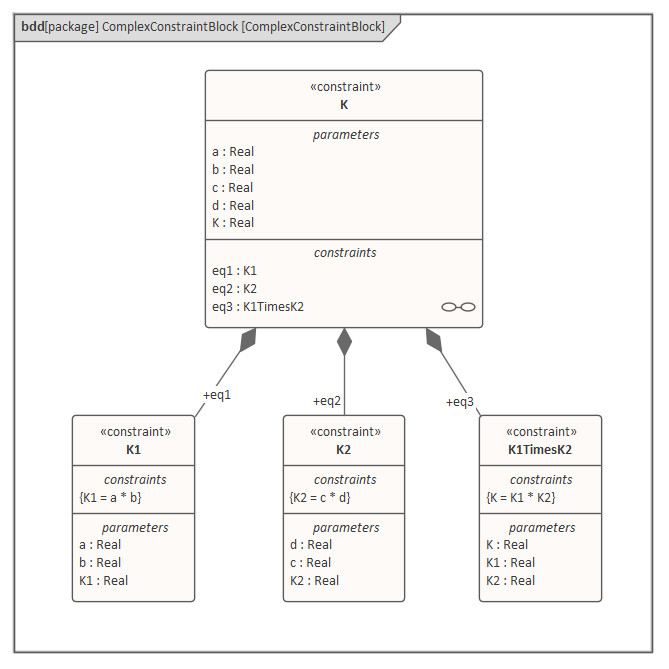
系统不会从一次计算中提取K的值,而是首先计算 K1,然后是 K2,最后是 K1 和 K2 的乘积,给出K的值。
这种结构还可以更轻松地修改计算中某些元素的输入,而不会影响其他元素。

